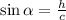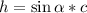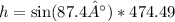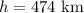To find the distance between UFP and A, we need to calculate c.
Now, remember that the sum of the 3 internal angles of a triangle is equal to 180°.
So find angle B
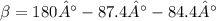
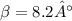
Now with the law of sines calculate c:
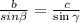
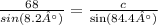
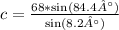
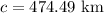
So the distance from A is 474.49 km
Now use this triangle to find h
You know the hypotenuse, which is equal to c=474.49km