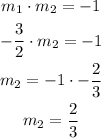Question

What the slope of a line perpendicular to one with points (6,-5) and (2,1).

Answer 1

First, we need to find the slope of the line that passes through the points (6,-5) and (2,1).

The slope (m) of the line that passes through the points (x1, y1) and (x2, y2) is calculated as follows:

`m=(y_2-y_1)/(x_2-x_1)_{}`

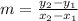
Replacing with the points (6,-5) and (2,1), we get:

`m_1=(1-(-5))/(2-6)=(6)/(-4)=-(3)/(2)`

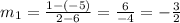
Two lines are perpendicular when the multiplication of their slopes is equal to minus one. Then, the slope (m2) of a line perpendicular to one with points (6,-5) and (2,1) is:

`\begin{gathered} m_1\cdot m_2=-1 \\ -(3)/(2)\cdot m_2=-1 \\ m_2=-1\cdot-(2)/(3) \\ m_2=(2)/(3) \end{gathered}`