To find the mean of a frequency distribution with intervals, we first need to find the midpoint of each interval.
We do that by adding the limits of each interval and dividing by 2:
1
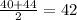
2
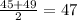
3
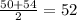
4
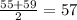
5
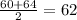
Now, we multiply these midpoints by the frequency of each interval and sum them:
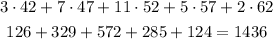
Now, we divide this sum by the sum of the frequencies, and this will be the mean.
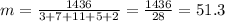
So, the mean calculated by using the frequency distribution is 51.3, which is lower than the actual mean of the data, 56.3.