According to the Kinetic Theory of Gases, a gas can be modeled as being formed by small molecules relative to the distance between them, that barely interact with each other but bounce at the walls of the container.
Each time that a molecule bounces at the walls, there is a change in the linear momentum of the molecule that must be provided by a force being applied on the molecule by the walls. From Newton's Third Law of Motion we can deduce that a force is also applied by the molecules on the walls.
Since we can think on the walls of the container as having a definite area, the Kinetic Theory of Gases allows us to calculate the average force that is exerted over the walls, and then, we can deduce the pressure inside the container in terms of the mass of the molecules and the average speed of the molecules.
The frequency with which the molecules hit the walls of the container depends on the size of the container: If the container is larger for a given amount of molecules with a fixed average speed, then the molecules have to travel a greater distance before they hit a wall again, then, there are less impacts per unit time, so, the average force exerted on the walls will be less and so will the pressure. A smaller container allows the molecules to hit the walls more often, hence creating a greater pressure.
Experimentally, these reasonings are confirmed by a result known as the ideal gas law, which relates the pressure P, the volume V, the temperature T and the amount of substance n of a gas as follows:
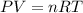
Where R is a constant called the universal gas constant:
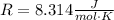
If we isolate P from the equation, we can see that the pressure of a gas is inversely proportional to the volume of its container:
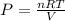
A smaller container for a fixed temperature and amount of substance will have a greater pressure. Similarly, if the same amount of substance of a gas at the same temperature is kept in a greater container, the pressure will be lower.
On the other hand, the temperature of a gas is related to the average kinetic energy of the molecules of the gas, so an exchange of energy is required to create processes where a change in temperature causes a change in the volume of the container at constant pressure.