Question

Try It 2 What is the equation of the line that passes through (2, -1) and (1,3)? Step 1: Solve the slope using the slope formula Y2-yi X2-X m Step 2: Write the equation in point-slope form y - Y, 7 m(x-*

Answer 1

Given the points (2,-1) and (1,3), we find the slope of the line that passes through them with the formula:

`m=(y_2-y_1)/(x_2-x_1)`

Then, in this case we have:

`\begin{gathered} (x_1,y_1)=(2,-1) \\ (x_2,y_2)=(1,3) \\ \Rightarrow m=(3-(-1))/(1-2)=(3+1)/(-1)=(4)/(-1)=-4 \\ m=-4 \end{gathered}`

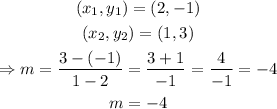
We have that the slope is -4. Now we use the first point to write the equation of the line in point-slope form:

`\begin{gathered} (x_1,y_1)=(2,-1) \\ m=-4 \\ y-y_1=m\cdot(x-x_1) \\ \Rightarrow y-(-1)=-4\cdot(x-2) \\ y+1=-4\cdot(x-2) \end{gathered}`

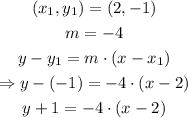
therefore, the equation in point-slope form is y+1=-4(x-2)