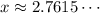Question

Solve without using a calculator nor natural logarithms (e or in)

Answer 1

Hello there. To solve this question, we'll have to remember some properties about exponential equations.

Given the following equation:

`2^(3x-4)=5\cdot3^(-x+4)`

To solve it, take the base 10 logarithm on both sides of the equation:

`\log(2^(3x-4))=\log(5\cdot3^(-x+4))`

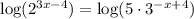
Apply the following properties:

`\begin{gathered} 1.\text{ }\log(a\cdot\,b)=\log(a)+\log(b) \\ \\ 2.\text{ }\log(a^b)=b\cdot\log(a) \end{gathered}`

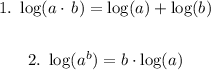
Therefore we get

`(3x-4)\cdot\log(2)=\log(5)+(4-x)\cdot\log(3)`

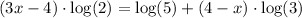
Apply the FOIL, such that we get

`3\log(2)\,x-4\log(2)=\log(5)+4\log(3)-\log(3)\,x`

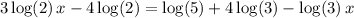
Add log(3) x + 4 log(2) on both sides of the equation, such that we get

`3\log(2)\,x+\log(3)\,x=\log(5)+4\log(3)+4\log(2)`

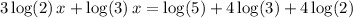
Rewrite

`\begin{gathered} 3\log(2)=\log(2^3)=\log(8) \\ \\ 4\log(3)=\log(3^4)=\log(81) \\ \\ 4\log(2)=\log(2^4)=\log(16) \\ \end{gathered}`

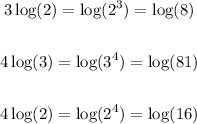
Therefore we get

`\begin{gathered} (\log(8)+\log(3))x=\log(5)+\log(81)+\log(16) \\ \\ \Rightarrow\log(24)\,x=\log(6480) \end{gathered}`

Divide both sides of the equation by a factor of log(24)

`x=(\log(6480))/(\log(24))`

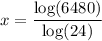
This is the answer to this question and it is approximately equal to:

`x\approx2.7615\cdots`