We have to write an equation with an absolute value that will give the same answer for x=8 and x=14.
We can write a generic equation with a parameter and then find its value:
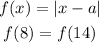
Then:

One of the two arguments, "8-a" or "14-a", has to be negative and the other positive. It must be "8-a" because if "14-a" were negative, then "8-a" would be also negative and there is no value of a that can make the two terms equal.
Then, we can rewrite the equality as:
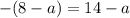
we then can solve for "a" as:

Note that x=11 is the midpoint between x=8 and x=14.
Answer:
The absolute value function that gives the same value for x=8 and x=14 is f(x) = |x-11|