Question

I don’t really understand the subject, and I don’t want the whole page done :)), I just need one on each line so I can understand the subject!

Answer 1

1.

The given diagram represents a rectangular prism. As only one side of the base is given, we have to assu ftme that the base is a square.

Now, the total surface area of the prism will be the sum of the areas of all its faces.

Also note that each side face of the prism is a triangle with base 9 ft and height 7 ft.

So the area of a triangular side face is calculated as,

`\begin{gathered} A_s=(1)/(2)\cdot9\cdot7 \\ A_s=(63)/(2) \\ A_s=31.5 \end{gathered}`

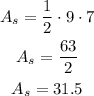
Since base is a square of side 9 ft, its area is given by,

`\begin{gathered} A_b=9\cdot9 \\ A_b=81 \end{gathered}`

Since each side face is identical, the total lateral surface area is given by,

`\begin{gathered} \text{LSA}=4\cdot A_s \\ \text{LSA}=4\cdot(31.5) \\ \text{LSA}=126 \end{gathered}`

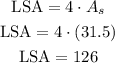
Then the total surface area of the given prism is calculated as,

`\begin{gathered} TSA=LSA+\text{Base Area} \\ \text{TSA}=126+81 \\ \text{TSA}=207 \end{gathered}`

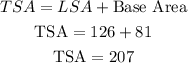
Thus, the area of the of the given prism is 207 square feet.