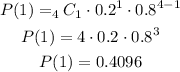Question

A parent-teacher committee consisting of 4 people is to be formed from 20 parents and 5 teachers find the probability that the committee will consist of these people. (Assume that the selection will be random) a) all teachersB) 2 teachers and 2 parents c) all parents d) I teacher and 3 parents

Answer 1

This situation can be modeled with the binomial distribution if we consider each person as a teacher or not a teacher.

The probability that a person is a teacher is computed as follows:

`p=\frac{\text{ number of teachers}}{total\text{ number of people}}=(5)/(20+5)=0.2`

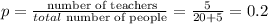
The binomial distribution formula is:

`P(x)=_nC_x\cdot p^x\cdot q^(n-x)`

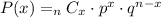
where:

P: binomial probability

x: number of times for a specific outcome within n trials

nCx: combinations

p: probability of success on a single trial (in this case, success means the person is a teacher)

q: probability of failure on a single trial (computed as 1 - p)

n: number of trials

a) Substituting with x = 4, n = 4, p = 0.2, q = 0.8 (= 1 - 0.2), we get:

`\begin{gathered} P(4)=_4C_4\cdot0.2^4\cdot0.8^(4-4) \\ P(4)=1\cdot0.2^4\cdot1 \\ P(4)=0.0016 \end{gathered}`

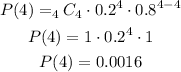
b) Substituting with x = 2, n = 4, p = 0.2, q = 0.8 (= 1 - 0.2), we get:

`\begin{gathered} P(2)=_4C_2\cdot0.2^2\cdot0.8^(4-2) \\ P(2)=6\cdot0.2^2\cdot0.8^2 \\ P(2)=0.1536 \end{gathered}`

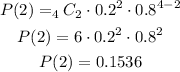
c) Substituting with x = 0, n = 4, p = 0.2, q = 0.8 (= 1 - 0.2), we get:

`\begin{gathered} P(0)=_4C_0\cdot0.2^0\cdot0.8^(4-0) \\ P(0)=1\cdot1\cdot0.8^4 \\ P(0)=0.4096 \end{gathered}`

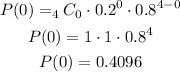
d) Substituting with x = 1, n = 4, p = 0.2, q = 0.8 (= 1 - 0.2), we get:

`\begin{gathered} P(1)=_4C_1\cdot0.2^1\cdot0.8^(4-1) \\ P(1)=4\cdot0.2^{}\cdot0.8^3 \\ P(1)=0.4096 \end{gathered}`