Question

ДАВС - ADEF. Find the measure of the given angles.mZA= x +22mZD = 2x

Answer 1

The problem stated that triangles ABC and DEF are congruent, which means that angle A on triangle ABC and angle D on triangle DEF are also congruent. Hence, we have

`m\angle D\cong m\angle A`

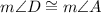
Substitute the given algebraic equations describing the measurements of the angles on the equation above, we have

`2x=x+22`

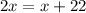
Solve for x

`\begin{gathered} 2x-x=22 \\ x=22 \end{gathered}`

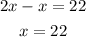
Hence, the measurement of angle A is

`\begin{gathered} m\angle A=22+22 \\ m\angle A=44 \end{gathered}`

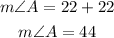
Answer: 44 degrees