Question

Solve the following system of equations using an inverse matrix. You must alsoindicate the inverse matrix, A-1, that was used to solve the system. You mayoptionally write the inverse matrix with a scalar coefficient.-4x+10y = -2-x+ 2=-3.

Answer 1

The coefficient matrix A is,

`A=\begin{bmatrix}-4 & 10 \\ -1 & 2\end{bmatrix}`

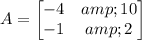
The constant matrix B is,

`B=\begin{bmatrix}-2 \\ -3\end{bmatrix}`

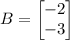
We have the equation,

`AX=B`

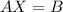
Solving for X, we have,

`\begin{gathered} AX=B \\ X=A^(-1)B \end{gathered}`

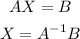
Now, if we have a 2 x 2 matrix of the form,

`A=\begin{bmatrix}a & b \\ c & d\end{bmatrix}`

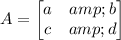
The inverse of this matrix is given by the formula,

`A^(-1)=(1)/(ad-bc)\begin{bmatrix}d & -b \\ -c & a\end{bmatrix}`

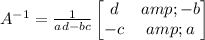
So, let's find the inverse matrix using this formula. Shown below:

`\begin{gathered} A^(-1)=(1)/(ad-bc)\begin{bmatrix}d & -b \\ -c & a\end{bmatrix} \\ A^(-1)=(1)/(-8--10)\begin{bmatrix}2 & -10 \\ 1 & -4\end{bmatrix} \\ A^(-1)=(1)/(2)\begin{bmatrix}2 & -10 \\ 1 & -4\end{bmatrix} \\ A^(-1)=\begin{bmatrix}1 & -5 \\ (1)/(2) & -2\end{bmatrix} \end{gathered}`

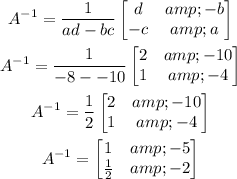
Now, we calculate X,

`\begin{gathered} X=A^(-1)B \\ X=\begin{bmatrix}1 & -5 \\ (1)/(2) & -2\end{bmatrix}\begin{bmatrix}-2 \\ -3\end{bmatrix} \\ X=\begin{bmatrix}(1)(-2)+(-5)(-3) \\ ((1)/(2))(-2)+(-2)(-3)\end{bmatrix} \\ X=\begin{bmatrix}-2+15 \\ -1+6\end{bmatrix} \\ X=\begin{bmatrix}13 \\ 5\end{bmatrix} \end{gathered}`

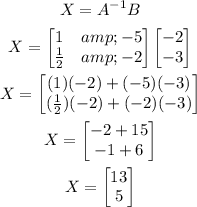
Thus, the solution of the system is >>>

x = 13y = 5