Question

If a square root parent function is vertically stretched by a factor of 6, what isthe equation of the new function, G(x)?A. G(x) = 65B. G(x) =-6/C. G(x) = V6xO D. G(x) == VE=

Answer 1

When a function f(x) is stretched vertically by a factor of an integer n, it implies that the new function g(x) is n times its old function.

Thus,

`g(x)=n* f(x)`

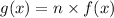
Given a square root function, we have

`f(x)=\sqrt[]{x}`

When the function is stretched by a factor of 6, let the new function be represented as G(x). This implies that

`\begin{gathered} G(x)=6* f(x) \\ =6*\sqrt[]{x} \\ \Rightarrow G(x)=6\sqrt[]{x} \end{gathered}`

Hence, the new function G(x) will be expressed as

`G(x)=6\sqrt[]{x}`

The correct option is A.