In order to determine whether the equations are parallel, perpendicular, or neither, let's simply each equation into a slope-intercept form or basically, solve for y.
Let's start with the first equation.
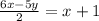
Cross multiply both sides of the equation.
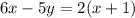
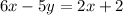
Subtract 6x on both sides of the equation.
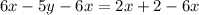
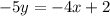
Divide both sides of the equation by -5.
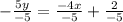
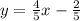
Therefore, the slope of the first equation is 4/5.
Let's now simplify the second equation.
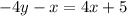
Add x on both sides of the equation.
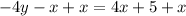
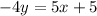
Divide both sides of the equation by -4.
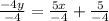
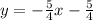
Therefore, the slope of the second equation is -5/4.
Since the slope of each equation is the negative reciprocal of each other, then the graph of the two equations is perpendicular to each other.