Question

I need to know the real solution for acts and the imaginary solutions

Answer 1

`\begin{gathered} \text{Given} \\ 4x^4=32x^3-68x^2 \end{gathered}`

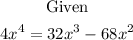
Equate the to zero, such that all the terms on the right side is transposed to the left side.

`\begin{gathered} 4x^4=32x^3-68x^2 \\ 4x^4-32x^3+68x^2=0 \\ \\ \text{Factor out all the GCF of all the terms which is }4x^2 \\ 4x^4-32x^3+68x^2=0 \\ 4x^2(x^2-8x+17)=0 \end{gathered}`

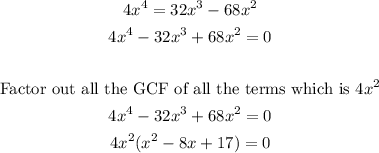
Apply the quadratic formula to the quadratic term.

`\begin{gathered} x^2-8x+17=0 \\ \text{where} \\ a=1,b=-8,c=17 \\ \\ x=( -b \pm√(b^2 - 4ac))/( 2a ) \\ x=( -(-8) \pm√((-8)^2 - 4(1)(17)))/( 2(1) ) \\ x=( 8 \pm√(64 - 68))/( 2 ) \\ x=( 8 \pm√(-4))/( 2 ) \\ x=( 8 \pm2\, i)/( 2 ) \\ x=( 8 )/( 2 )\pm(2\, i)/( 2 ) \\ \\ x=( 8 )/( 2 )+(2\, i)/( 2 ) \\ x=(8)/(2)+(2i)/(2) \\ x=4+i \\ \\ x=(8)/(2)-(2i)/(2) \\ x=(8)/(2)-(2i)/(2) \\ x=4-i \end{gathered}`

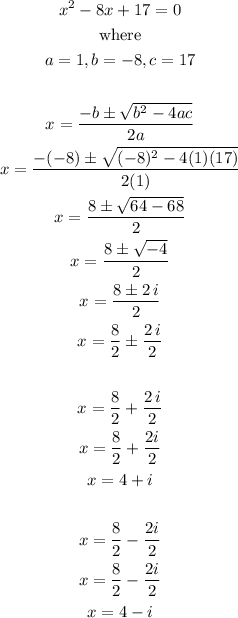
Now we have 2 solutions, solve for the other solution which is the solution for 4x².

`\begin{gathered} \text{Equate to zero} \\ 4x^2=0 \\ (4x^2)/(4)=(0)/(4) \\ x^2=0 \\ \sqrt[]{x^2}=\sqrt[]{0} \\ x=0 \end{gathered}`

Summarizing the solution.

`\begin{gathered} \text{The real solution for }x\text{ is }0, \\ \text{and the imaginary solution are }4\pm1i \end{gathered}`