The rate of change of a line is regarded as the slope/ gradient (m) of the line
The slope/ gradient (m) of the line moving through points (x₁,y₁) and (x₂,y₂) is given as
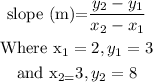
On substituting the above values in the formula above we will have the slope to be
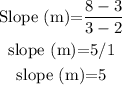
Therefore,
The rate of change of the line through (2,3) and (3,8) is 5