Given: A function
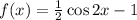
Required: Zeroes of the function in the interval [0,2π]
Step-by-step explanation:
For zero of the function f(x)
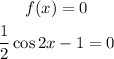
Now,
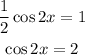
Now, cos function alsways lies between [-1,1].
It is not equal to 2 in the interval [0,2π].
Hence, the zeroes does not exist in this interval.
Final Answer: The correct answer is option 1.