Question

Kayla wanted to lose some weight, so she planned a day of exercising. She spent a total of 3 hours riding her bike and jogging. She biked for 3 miles and jogged for 5 miles. Her rate for jogging was 4 mph less than her biking rate. What was her rate when jogging?

Answer 1

Given:

Total time spends = 3 hours

Distance covered by bik = 3 miles

Distance covered by Jogging = 5 miles.

Her rate for jogging was 4 mph less than her biking rate.

Required- her rate when jogging.

Step-by-step explanation:

Let her rate when jogging be x mph.

Given that her rate for jogging was 4 mph less than her biking rate.

So, her rate when biking will be:

`\begin{gathered} Rate\text{ when jogging =Rate of biking -4} \\ x=Rate\text{ of biking -4} \\ Rate\text{ of biking =}(x+4)mph \end{gathered}`

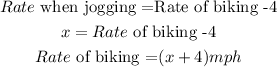
Now, the formula for the distance is:

`\begin{gathered} \text{ Distance=Rate}* time \\ \\ \Rightarrow Time=(Distance)/(Rate) \end{gathered}`

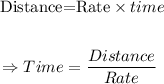
The total time spend is 3 hours. So, we have the equation:

`\begin{gathered} Time\text{ take by biking+Time take by jogging=total time} \\ \\ \frac{Distance\text{ covered by biking}}{Rate\text{ of biking}}+\frac{Distance\text{ covered by jogging}}{Rate\text{ of jogging}}=3\text{ hours} \\ \\ (3)/(x+4)+(5)/(x)=3 \end{gathered}`

Solving further, we have:

`\begin{gathered} (3x+5(x+4))/(x(x+4))=3 \\ \\ 3x+5x+20=3x(x+4) \\ \\ 8x+20=3x^2+12x \\ \\ 3x^2+12x-8x-20=0 \\ \\ 3x^2+4x-20=0 \end{gathered}`

Now, solving the quadratic equation.

`\begin{gathered} 3x^2+4x-20=0 \\ \\ 3x^2-6x+10x-20=0 \\ \\ 3x(x-2)+10(x-2)=0 \\ \\ (x-2)(3x+10)=0 \end{gathered}`

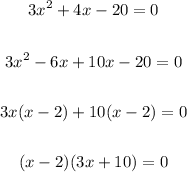
Now, we find the value of x by equating the factors by zero.

`\begin{gathered} x-2=0 \\ x=2 \end{gathered}`
`\begin{gathered} 3x+10=0 \\ 3x=-10 \\ x=(-10)/(3) \end{gathered}`

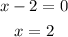
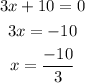
Here, x=2 and -10/3.

We know that the rate cannot be in negative. So, we neglect the negative value of x.

Taking x=2 into account.

So, her rate when jogging is 2mph.

Final answer: Her rate when jogging is 2 mph.