Question

consider the following equation.2y-2= -2(4-x)What is the equation of the line that passes through the point (-15,-2) and is parallel to the given line. Make the answer in slope-intercept form

Answer 1

Given the equation of the line:

`2y-2=-2\mleft(4-x\mright)`

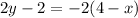
Since we asked on the equation of the line that is parallel to the line of equation 2y-2= -2(4-x), the lines must have the same slope since they are said to be parallel.

2y-2= -2(4-x) is in Point-Slope Form, with standard form of:

`y-y_1_{}=m(x-x_1)`

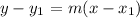
Where,

m = the slope of the line

Therefore, the slope of the lines must be -2.

Let's now find out the equation of the parallel line in Slope-Intercept Form.

Step 1: Substitute m = -2 and x,y = (-15,-2) in y = mx + b to find the y-intercept (b).

`\text{ y = mx + b}`
`\text{ -2 = -2(-15) + b}`
`\text{ -2 = 30 + b}`
`\text{ -2 - 30 = b}`
`\text{ -32 = b }\rightarrow\text{ b = -32}`

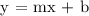
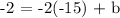
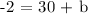
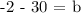
Step 2: Let's complete the equation. Substitute m = -2 and b = -32 in y = mx + b.

`\text{ y = mx + b}`
`\text{ y = (-2)x + (-32)}`
`\text{ y = -2x - 32}`

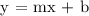
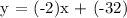
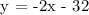
Therefore, the equation of the line parallel to 2y-2= -2(4-x) in Slope-Intercept From is y = -2x - 32.