Question

Solve for x. 16/7x 4x+4/8x-3 X= (Type an integer or a simplified fraction. Use a comma to separate answers as needed.)

Answer 1

EXPLANATION

Considdering the given triangle, we can assevere by the Triangle Proportionality Theorem that there are two similar triangles, and therefore the following relationship is fullfiled:

`(16)/(7x)=(4x+4)/(8x-3)`

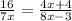
Multiplying both sides by 7x:

`16=7x(4x+4)/(8x-3)`

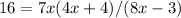
Multiplying both sudes by 8x-3:

`16(8x-3)=7x(4x+4)`

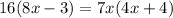
Applying the distributive property:

128x - 48 = 28x^2 + 28x

Subtracting -(28x^2 +28x) to both sides:

128x - 48 - 28x^2 - 28x = 0

Adding and rearranging terms:

-28x^2 +100x - 48

Solving with the quadratic formula:

`x_1,x_2=\frac{-100\pm\sqrt[]{100^2-4(-28)(-48)}}{2\cdot-28}`

Simplifying:

`x_1,x_2=(-100\pm68)/(-56)`

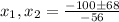
The roots are x_1= 4/7 and x_2 = 3

Just one is the valid option, so considering x=4/7 and replacing in the given equation:

7*4/7 = 4

8* 4/7 - 3 = 11/7

Now, trying with x=3:

7*3 = 21

8*3 -3 = 21 (This is not a viable solution because the Hypotenuse can not be the same as the adjacent leg, so the solution is x=4/7.

The answer is x=4/7