The function
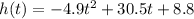
Gives us the position of the cannonball measured from the ground at a time t.
When h(t)=0, the cannonball will strike the ground. Therefore,
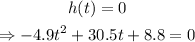
Solving for t using the quadratic equation formula
![\Rightarrow t=\frac{-30.5\pm\sqrt[]{30.5^2-4(-4.9)(8.8)}}{2\cdot-4.9}=(-30.5\pm33.2074)/(-9.8)](https://img.qammunity.org/2023/formulas/mathematics/college/18xbt5ynpimrcup053efguz1xyrp92d7ra.png)
Then,
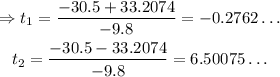
It makes no sense that the cannonball reaches the ground before we shoot it; therefore, t_1 cannot be the answer. The only remaining possibility is t=6.5seconds
The answer is 6.5 seconds.