The given system is
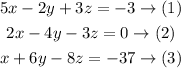
Use equation (3) to find x in terms of y and z
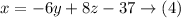
Substitute x in (1) and (2) by (4)
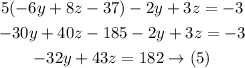
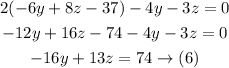
Multiply (6) by 2
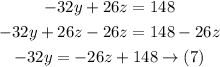
Substitute -32y in (5) by (7)
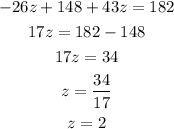
Substitute the values of z in equation (7) to find y
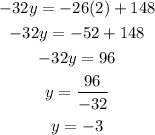
Substitute the values of z and y in equation (4) to find x
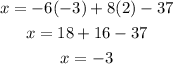
The solution is x = -3, y = -3, z = 2