Answer:
Step-by-step explanation:
The general expression of a quadratic equation is;
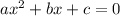
Given the quadratic expression
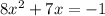
Firstly, we need to re-arrange and equate the expression to zero.
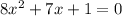
To factorize this expression, we will use the general formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
From the expression given, we can see that a = 8, b = 7 and c = 1
Substitute these values into the general formula as shown:
![\begin{gathered} x=\frac{-7\pm\sqrt[]{7^2-4(8)(1)}}{2(8)} \\ x=\frac{-7\pm\sqrt[]{49-32}}{16} \\ x=\frac{-7\pm\sqrt[]{17}}{16} \\ x=(-7\pm4.123)/(16) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/en3fq5pjihvvr05k4n2zqkmofka4xlngbz.png)
Get the required values of x:
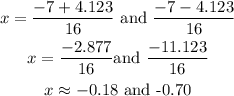
This shows that the solution to the quadratic equation is (-0.18, -0.70)