Given:
The line passes through point (7,-3) and perpendicular to line 2x-5y-8=0.
Step-by-step explanation:
Simplify the equation 2x-5y-8=0 in slope intercept form.

So slope of line is 2/5.
Determine the slope of perpendicular line.
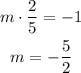
The equation of line with slope m = -5/2 is,
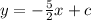
Substitute 7 for x and -3 for y in the equation y = -5/2x + c to determine the value of c.
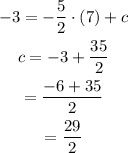
The value of c is 29/2.
The equation of line is,
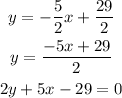
So answer is 2y + 5x -29 = 0