Question

OF bisects XEOG. MZEOF=(2x-3) and mZFOG =(x+10)°. What is the value of x. G 0

Answer 1

Let's begin by listing out the information given to us:

OF bisects |EOG|: we have |EOF| & |FOG|

|EOF| = 2x - 3; |FOG| = x + 10

Both |EOF| & |FOG| are equal because OF is the midpoint

To solve for the value of x, we equate |EOF| & |FOG|, we have:

`\begin{gathered} |EOF|=|FOG|\Rightarrow2x-3=x+10 \\ 2x-x=10+3 \\ x=13 \end{gathered}`

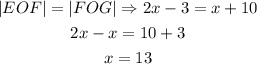
x = 13