To calculate the accrued amount of an account that compounds continuously you have to apply the following formula:
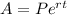
Where
A is the accrued or final amount
P is the principal or initial amount
r is the interest rate expressed as a decimal value
t is the time period in years
You have to determine the principal amount given that after 9 years the final balance of an account that has an annual interest of 8% is $18,091.34
- The first step is to write the formula for the principal amount P, to do so, divide both sides of the expression by e^(rt)
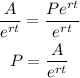
- Next, divide the interest rate by 100 to express it as a decimal value
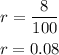
- Now you can calculate the principal amount, replace the expression using A=18,091.34, r=0.08, and t=9
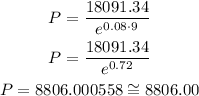
The initial amount of the investment was $8806