Question

Two sides of a triangle are 8 inches and 12 inches.Find the area of the triangle if the hypotenuse is 12 inches and the leg is 8 inches.

Answer 1

`35.76in^2`

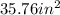
Step-by-step explanation

The hypotenuse of the triangle is 12 inches and one leg is 8 inches.

The area of a triangle is:

`\begin{gathered} A=(1)/(2)\cdot b\cdot h \\ b=\text{base; h}=\text{height} \end{gathered}`

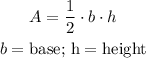
To find the area of the triangle, find the other leg first: using Pythagoras Rule:

`\begin{gathered} hyp^2=a^2+b^2 \\ a,b\text{ =legs of triangle} \\ \Rightarrow12^2=8^2+x^2 \\ 144=64+x^2 \\ x^2=144-64=80 \\ x=\sqrt[]{80} \\ x=8.94in \end{gathered}`

Find the area of the triangle:

`\begin{gathered} A=(1)/(2)\cdot8\cdot8.94 \\ A=35.76in^2 \end{gathered}`

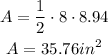
That is the area of the triangle.