Given:
Teenagers who own a game console = 46%
Teenagers who own a personal computer = 35%
Teenagers who own both a game console and personal computer = 29%
Required- the conditional probability that a teenager randomly selected owns a game console, given that the teenager owns a personal computer.
Step-by-step explanation:
Let A be the event that the teenager randomly selected owns a game console.
Let B be the event the teenager randomly selected owns a personal computer.
Now, we change the probability of each event in decimal as:
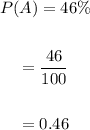
Now, the probability of event B is:
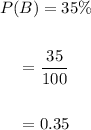
Now, the probability of events A and B is:
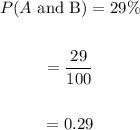
We know that the formula to find the conditional probability of event A, given event B is:
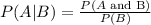
Now, we put the given values in the formula, we get:

Final answer: The conditional probability that a teenager randomly selected owns a game console, given that the teenager owns a personal computer is approximately 0.83.