Question

Tickets for a dance recital cost $24 for adults and $6 dollars for children. The dance company sold 229 tickets and the total receipts were $3,264. How many adult tickets and how many child tickets were sold?

Answer 1

Let:

a be the number of adults.

c be the number of children.

To solve this question, follow the steps below.

Step 01: Write an equation for the total of tickets sold.

Since the company sold 229 tickets for adults and children:

`a+c=229`

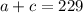
Step 02: Write an equation for the total receipts.

The total receipt of $3,264 is the sum of the receipts from the adults' tickets and the children's ticket.

Then,

`24a+6c=3,264`

Step 03: Isolate a in the first equation and substitute it in the second equation.

`a+c=229`

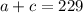
To isolate a, subtract c from both sides.

`\begin{gathered} a+c-c=229-c \\ a=229-c \end{gathered}`

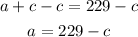
Substituting a in the second equation:

`24\cdot(229-c)+6c=3,264`

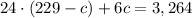
And solving the equation for c:

`\begin{gathered} 24\cdot229-24\cdot c+6c=3,264 \\ 5,496-18c=3,264 \\ \end{gathered}`

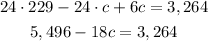
Subtracting 5,496 from both sides:

`\begin{gathered} 5,496-18c-5,496=3,264-5,496 \\ -18c=-2,232 \end{gathered}`

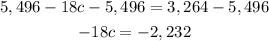
And dividing both sides by -18:

`\begin{gathered} (-18)/(-18)c=(-2,232)/(-18) \\ c=124 \end{gathered}`

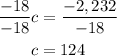
Step 04: Use the value of c to find a.

`\begin{gathered} a=229-124 \\ a=105 \end{gathered}`

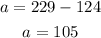
Answer:

Adult tickets sold: 109.

Chil tickets sold: 124.