Question

The time required for an outlet pipe to empty a tank is inversely proportional to the cross-sectional area of 113.0 sq in. Requires ‘6.4 hours to empty a certain tank. If the pipe was replaced with one with a cross-sectional area of 50.25 sq in., how long would it take this pipe to empty the same tank?

Answer 1

hello

the relationship between the time and the area of the pipe is an inversely proportional one

`\begin{gathered} t\propto(1)/(a) \\ t=(k)/(a) \\ k=ta \\ t_1a_1=t_2a_2 \end{gathered}`
`\begin{gathered} a_1=113in^2 \\ t_1=6.4h \\ a_2=50.25in^2 \\ t_2=\text{ ?} \end{gathered}`

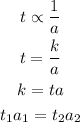
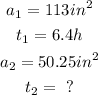
above are the value of data given in the question

we can now proceed to solve this problem using the formula we've already established.

`\begin{gathered} t_1a_1=t_2a_2 \\ 113*6.4=t_2*50.25 \\ 723.2=50.25t_2 \\ \text{divide both sides by the coefficient of t\_2} \\ (723.2)/(50.25)=(50.25t_2)/(50.25) \\ t_2=14.39h \end{gathered}`

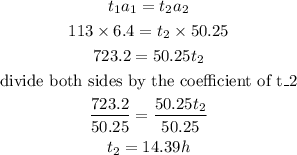
from the calculations above, decreasing the cross-sectional area to 50.25sq in, would increase the time it takes for the tank to empty to 14.39 hours