Question

Construct a polar equation for the conic section with the focus at the originand the following eccentricity and directrix.ConicEccentricityDirectrixparabolae=X =

Answer 1

Given:

Here the eccentricity and directrix are 1 and -1/3 respectively of parabola .

Required:

We have to construct a polar equation for the parabola

Step-by-step explanation:

Formula to construct the polar equation is

`\Gamma=(ep)/(1+ecos\emptyset)`
`\Gamma=(1*(1)/(3))/(1+1cos\emptyset)`
`\Gamma=(1)/(3+3cos\emptyset)`

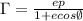
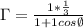
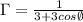
Final answer:

`\Gamma=(1)/(3+3cos\emptyset)`

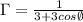
is the polar equation for given information.