Question

Joachim draws a circle with the equation 1? + y = 4. Then he draws the line

Answer 1

Step 1: Problem

Check the problem on the left-hand side.

Step 2: Concept

Find the center and radius of the circle from the equation of the circle and draw the circle.

Step 3: Method

`\begin{gathered} \text{From} \\ x^2+y^2\text{ = 4} \\ x^2+y^2=2^2 \\ \text{Compare with the general equation of a circle with center at the origin 0.} \\ x^2+y^2=r^2 \\ \text{center = (0,0) and radius r = 2} \\ \end{gathered}`

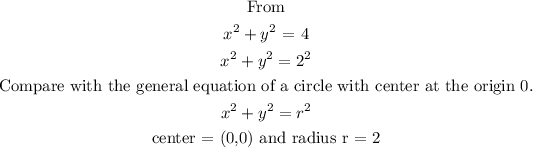
Then find the value of y using Pythagoras theorem.

Opposite = y

Hypotenuse = 2

Adjacent = 1

`\begin{gathered} \text{Opposite}^2+Adjacent^2=Hypotenuse^2 \\ y^2+1^2=2^2 \\ y^2\text{ + 1 = 4} \\ y^2\text{ = 4 - 1} \\ y^2\text{ = 3} \\ y\text{ = }\sqrt[]{3} \end{gathered}`

Step 4: Final answer

The line x = 1 intercept the circle at

`(1\text{ , }\sqrt[]{3}\text{ ) and }(\text{ 1 , -}\sqrt[]{3)}`

Option D is the correct answer.