Question

Question is in photo the number 31 has nothing to do with the question

Answer 1

The Solution:

Given the lengths below:

We are required to investigate whether the lengths given above can be the sides lengths of a triangle.

Step 1:

We shall apply the Triangle Inequality Theorem.

This theorem states that if the side lengths of a triangle are a, b and c, then the following holds:

`\begin{gathered} a+b>c \\ a+c>b \\ b+c>a \end{gathered}`

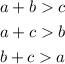
In this case,

Step 2:

Applying the triangle inequality theorem, we have

`10+12=22>20\text{ (condition satisfied)}`
`10+20=30>12\text{ (condition satisfied)}`
`12+20=32>10\text{ (condition satisfied)}`

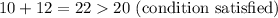
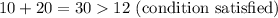
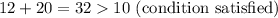
Thus, we shall conclude that it is possible for the given lengths to be side-lengths of a triangle since the set of lengths satisfies the triangle inequality theorem.

Therefore, the correct answer is: Yes, it is possible for the given set of lengths to be the sides of a triangle.