The situation is:
We need to find the length of the green line.
This is a right triangle, and we know the measure of the hyppotenuse, and an angle.
We can use the trigonometric relation cosine to find the distance from the firetruck to the building:
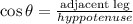
The distance between the truck and the buiding is the adjacent leg to the angle, let's call it x, then:
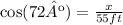
And we can solve for x:
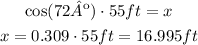
To the nearest whole foot, the distance between the firetruck and the building to reach the top of the building is 17ft