Question

Create a diagram of a ladder leaning on the side of a wall The wall is 16ft tall and the ladder is 18 ft long. What is the angle between the ladder and the ground?

Answer 1

62.73 degrees.

Explanation:

The diagram representing the given problem is attached below:

In the right triangle ABC above:

• The length of the ladder, AC = 18 ft

,

• The height of the wall, AB = 16 ft

,

• The angle between the ladder and the ground = x

From trigonometric ratios:

`\begin{gathered} \sin \theta=\frac{\text{Opposite}}{\text{Hypotenuse}} \\ \implies\sin x=(16)/(18) \end{gathered}`

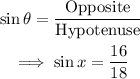
Next, take the arcsin of both sides:

`\begin{gathered} \implies x=\arcsin ((16)/(18)) \\ x=62.73\degree \end{gathered}`

The angle between the ladder and the ground is approximately 62.73 degrees.