Let's use the variable L to represent the length and W to represent the width.
If the length is 2 inches more than the width, we can write the following equation:
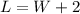
Then, if the area is equal to 15 in² and the area is given by the product of length and width, we have:
![\begin{gathered} A=L\cdot W \\ A=(W+2)\cdot W \\ 15=W^2+2W \\ W^2+2W-15=0 \\ W_1=\frac{-2+\sqrt[]{4+60}}{2}=(-2+8)/(2)=3 \\ W_2=(-2-8)/(2)=-5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/j7zaziioagpsi0kp6g6awyeg0klxd5r644.png)
Since the width can't be negative, we have W = 3.
Calculating L, we have:
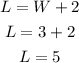
Therefore the length of the rectangle is 5 inches, while the width is 3 inches.