Question

A fair coin is flipped 3 times. What is the probability that the flips follow the exact sequence below?Flip One: HeadsFlip Two: HeadsFlip Three: TailsA. ⅛ B. ⅜ C. ⅓ D. ⅔E. ½

Answer 1

Given

A fair coin is flipped 3 times.

To find: What is the probability that the flips follow the exact sequence below?

Flip One: Heads

Flip Two: Heads

Flip Three: Tails

Step-by-step explanation:

It is given that,

A fair coin is flipped 3 times.

Then, the sample space is,

`\begin{gathered} S=\lbrace HHH,HHT,HTH,HTT,THH,TTH,THT,TTT\rbrace \\ n(S)=8 \end{gathered}`

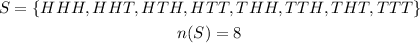
Let A be the event that the flips follow the sequence,

Flip One: Heads

Flip Two: Heads

Flip Three: Tails.

That implies,

`\begin{gathered} A=\lbrace HHT\rbrace \\ n(A)=1 \end{gathered}`

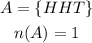
Therefore,

The probability that the flips follow the exact sequence is,

`\begin{gathered} P(A)=(n(A))/(n(S)) \\ =(1)/(8) \end{gathered}`

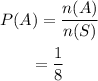
Hence, the answer is 1/8.