Question

Please help answer this problem for # 1. & 2.

Answer 1

1.

To determine the maximum number of kegs on the truck we need to find the volume of the truck and the kegs.

Since the truck is a prism, its volume is given by:

`V=lwh`

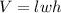
where l is the length, w is the width and h is the height. In this case the length is 7 ft, the width is 9 ft and the height is 53 ft. Then the volume of the truck is:

`\begin{gathered} V_T=(7)(9)(53) \\ V_T=3339 \end{gathered}`

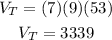
Hence, the volume of the truck is 3339 cubic ft.

The keg is a cylinder so its volume is:

`V_k=\pi r^2h`

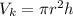
before we calculate the volume we need to change the measurements from inches to ft, so we need to remember that one ft is equal to 12 in. Then we have:

`\begin{gathered} 9\text{ in}\cdot\frac{1\text{ ft}}{12\text{ in}}=(3)/(4)\text{ ft} \\ \text{ And} \\ 32\text{ in}\cdot\frac{1\text{ ft}}{12\text{ in}}=(8)/(3)\text{ ft} \end{gathered}`

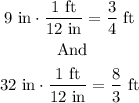
Now, that we have the measurements in ft we notice that the radius is 3/8 (half the diameter) and the height is 8/3, then the volume of each keg is:

`\begin{gathered} V_k=\pi((3)/(8))^2((8)/(3)) \\ V_k\approx1.1781 \end{gathered}`

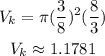
Hence, the volume of the kegs is 1.18 cubic ft.

Now, that the volume of the truck and of each keg we divide the volume of the truck by the volume of the keg to determine how many we can place in there:

`(V_T)/(V_k)=(3339)/(1.1781)=2834`

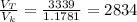
Therefore, we can place 2834 kegs in the truck.

2.

To determine the air space, we subtract the volume of each keg by the number we put on the truck to the volume of the truck:

`3339-(2834)(1.1781)=0.2646`

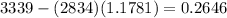
Therefore, the volume of air is 0.2646 cubic ft