Since the number of days is normally distributed, we can use a z-score table to find the percentage under a certain value in the distribution.
To do this, we first need to convert the value to a z-score by using:

Where z is the z-score, x is the value we want to convert, μ is the mean and σ is the standard deviation.
Since we want the bound value of 10 days, we will convert this to z-score:
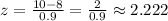
So, in a z-score table, we can consult the probability of having a value under a certain z-score. for this case, we have:
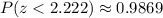
However, we want the probability, or the percentage, of patiens to get ill more than 10 days, in terms of z, this means:
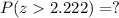
Since the whole normal distribution has a percentage of 100%, that is, 1, if we add the percentage less than and greater than 2.222, we wil have 1, so:
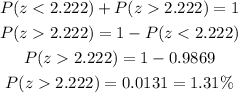
Which corresponds to alternative A.