Question

Given the definitions of f(c) and g(x) below, find the value of(gof)(-5).f(x) = 22+ 6x + 3g(x) = 2x + 8

Answer 1

This is an example of function composition. Being g and f well defined for the purpose of the composition and x in the domain of f, the composition is:

`g\circ f(x)=g(f(x))`

We can apply this definition to our problem.

Notice that, first, f(x) is calculated and then we used the result (let's called it y) and evaluate it using g (this is g(y))

So, regarding our problem

`\begin{gathered} f(x)=x^2+6x+3 \\ g(x)=2x+8 \\ \Rightarrow \\ f(-5)=(-5)^2+6(-5)+3=25-30+3=-2 \\ \Rightarrow \\ g\circ f(-5)=g(f(-5))=g(-2)=2(-2)+8=-4+8=4 \end{gathered}`

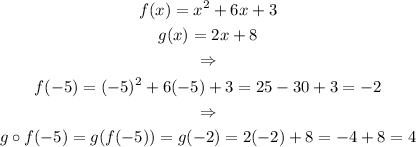
Then

`g\circ f(-5)=4`