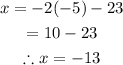Question

Find the solution of this system of equations -2y=-42-4x-x-2y=23

Answer 1

x = -13 and y = -5

Step-by-step explanation:

Given the below equations;

`\begin{gathered} -2y=-42-4x \\ -x-2y=23 \end{gathered}`

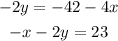
Let's go ahead and solve simultaneously using the substitution method.

From the 2nd equation;

`\begin{gathered} -x=2y+23 \\ \therefore x=-2y-23 \end{gathered}`

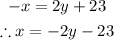
Let's put x = -2y - 23 into the 1st equation and find y;

`\begin{gathered} -2y=-42-4(-2y-23) \\ -2y=-42+8y+92 \\ -2y-8y=50 \\ -10y=50 \\ y=-(50)/(10) \\ \therefore y=-5 \end{gathered}`

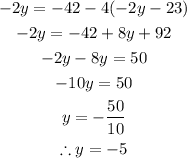
Let's substitute the value of y into x = -2y - 23 and find x;

`\begin{gathered} x=-2(-5)-23 \\ =10-23 \\ \therefore x=-13 \end{gathered}`