Question

Graph 3x+2y>120-Please be quick, I am in a hurry

Answer 1

So we must solve the following inequality:

`3x+2y>120`

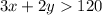
First we should substract 3x from both sides:

`\begin{gathered} 3x+2y-3x>120-3x \\ 2y>120-3x \end{gathered}`

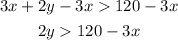
Then we divide both sides by 2:

`\begin{gathered} (2y)/(2)>(120-3x)/(2) \\ y>60-(3)/(2)x \end{gathered}`

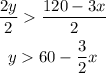
This basically means that the solution to this inequality is the region above the line y=60-(3/2)x. In order to graph it we first need to graph:

`y=60-(3)/(2)x`

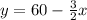
So we need at least two of its points. We can take x=0 and x=40 and find their corresponding y values:

`\begin{gathered} y=60-(3)/(2)\cdot0=60 \\ y=60-(3)/(2)\cdot40=60-60=0 \end{gathered}`

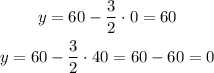
Then the line is the one that passes through both (0,60) and (40,0). The graph is given by this line (dashed because the inequality has a > sign) and a shaded region above it: