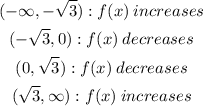Given the following function
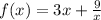
we want to calculate the critical points and the point where the function is not defined.
A rational function is not defined when the denominator is equal to zero, therefore, the value of B is 0.

The critical points are the zeros of the first derivative. Calculating the first derivative, we have:
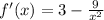
The zeros of the first derivative are:
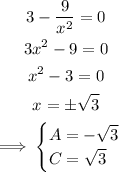
Those are the values of the critical points.
To find if the function is increasing or decreasing, we evaluate the one sided limits on the extremes of the intervals and compare the function values.
On the first interval:
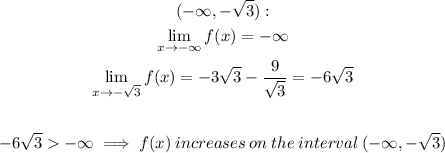
By the same logic, for the other intervals we have: