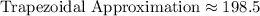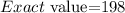Question

Use the Trapezoidal Rule to approximate ∫53(6x2+1) dx using n=4. Round your answer to the nearest tenth. Evaluate the exact value of ∫53(6x2+1) dx and compare the results.

Answer 1

Given:

`\int_3^5(6x^2+1)dx\text{ and n=4.}`

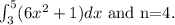
Required:

We need to find the trapezoid approximation and exact value.

Step-by-step explanation:

`Let\text{ f\lparen x\rparen=}6x^2+1.`

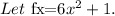
The given interval is {3,5} and n=4.

Consider the formula.

`\Delta x=(b-a)/(n)`

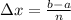
Substitute a=5, b=5, and n=4 in the formula,

`\Delta x=(5-3)/(4)=(2)/(4)=0.5`
`x_0=3,x_1=3.5,x_2=4,x_3=4.\text{5 and }x_4=5.`

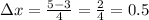
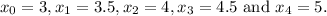
Consider the trapezoid formula.

`\int_a^bf(x)dx\approx(1)/(2)\Delta x(f(x_0)+2f(x_1)+2f(x_2)+2f(x_3)+f(x_4))`
`Substitute\text{ }\Delta x=0.5,x_0=3,x_1=3.5,x_2=4,x_3=4.\text{5 and }x_4=5\text{ in the formula,}`
`\int_3^5f(x)dx\approx(1)/(2)(0.5)(f(3)+2f(3.5)+2f(4)+2f(4.5)+f(5))`
`Use\text{ f\lparen x\rparen=}6x^2+1.`
`=(1)/(2)(0.5)((6(3)^2+1)+2(6(3.5)^2+1)+2(6(4)^2+1)+2(6(4.5)^2+1)+(6(5)^2+1)`
`=(1)/(2)(0.5)(55+149+194+245+151)`
`\int_3^5(6x^2+1)dx\approx198.5`

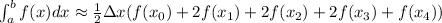
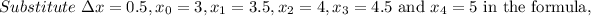
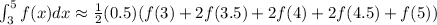
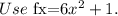
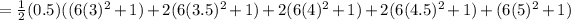
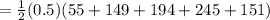
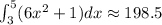
Consider the given integral.

`\int_3^5(6x^2+1)dx=\int_3^56x^2dx+\int_3^51dx`

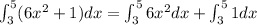
Integrate the given integral.

`\int_3^5(6x^2+1)dx=[(6x^3)/(3)]^5_3+[x]^5_3`
`=[2x^3]_3^5+[x]_3^5`
`=[2(5)^3-2(3)^3]+[5-3]`
`=198`
`\int_3^5(6x^2+1)dx=198`

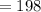
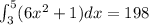
Final answer:

`\text{ Trapezoidal Approximation}\approx198.5`
`Exact\text{ value=198}`