Question

Consider the letters in the word "history". If one letter is drawn at random, find the probabilities of the events listed below. Assume y is not a vowel.a. Letter is a vowel.b. Letter is a consonant.

Answer 1

Given:

The letters of the word "history".

Required:

The probability that a selected letter,

a. Letter is a vowel.

b. The letter is a consonant.

Step-by-step explanation:

The sample space is given as,

`\begin{gathered} Sample\text{ space = }\lbrace\text{ h, i, s, t, o, r, y \textbraceright} \\ n(S)\text{ = 7} \end{gathered}`

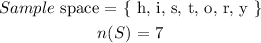
__(a)__

Assume A be the event the selected letter is a vowel.

The event A is given as,

`\begin{gathered} A\text{ = \textbraceleft i, o \textbraceright} \\ n(A)\text{ = 2} \end{gathered}`

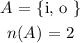
The required probability is calculated as,

`\begin{gathered} P(vowel)\text{ = }(n(A))/(n(S)) \\ P(vowel)\text{ = }(2)/(7) \\ P(vowel)\text{ = 0.2857} \end{gathered}`

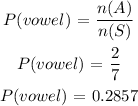
__(b)__

Assume B be the event that a selected letter is a consonant.

The event B is given as,

`\begin{gathered} B\text{ = \textbraceleft h, s, t, r, y \textbraceright} \\ n(B)\text{ = 5} \end{gathered}`

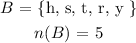
The required probability is calculated as,

`\begin{gathered} P(consonent)\text{ = }(n(B))/(n(S)) \\ P(consonent)\text{ = }(5)/(7) \\ P(consonent)\text{ = 0.7143} \end{gathered}`

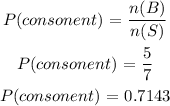
Answer:

(a) Thus the probability that a selected letter is a vowel is 0.2857.

(b) Thus the probability that a selected letter is a consonant is 0.7143.