Let:
• A, be the event of Bob choosing an used vehicle
,
• B, be the event of Bob choosing a car
Now, we know that:
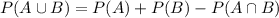
Out of the 41 vehicles, 18 are used. Therefore,
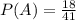
Out of the 41 vehicles, 19 are cars. This way,
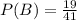
Out of the 41 vehicles, 8 are used cars. Thereby,
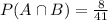
This way, we'll have that
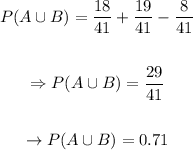
Therefore, the probability that the vehicle that Bob chooses is used or is a car is aproximately 0.71