Question

the graph shows the proportional relationship which equation matches the graphanswers A (y equals 12x) B (y equals 1/4 x)C (y equals 4X) D (y equals x)

Answer 1

The graph above represent a line. So its equation is a line equation with the following form:

y = mx + b EQUATION 1

where

m = slope

and

b = intercept with y-axis.

To find the equation of the line, we must first find the slope m. By definition, the slope m is given by:

`m\text{ = }\frac{Y2\text{ - Y1}}{X2-X1}`

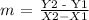
Here, (X1, Y1) represents the coordinates of a point A on the line. Also,

(X2,Y2) represent the coordinates of a point B on the line. That is:

A = (X1, Y1) and B = (X2,Y2)

So, if we take the points A = (1,4) = (X1, Y1) and B= (3,12) = (X2,Y2), and we substitute them in the slope equation, we have:

`m\text{ = }\frac{Y2\text{ - Y1}}{X2-X1}\text{ = }(12-4)/(3-1)\text{ = }(8)/(2)\text{ = 4}`

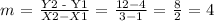
Then, the slope of our linear function is m = 4. So our new linear equation for the graph will be:

y = mx+b = 4x + b

that is:

y = 4x + b EQUATION 2

Now let's find the y-intercept = b. For that purpose, we take any point on the graph, for example A= (X,Y) = (1,4) and we substitute it in equation 2:

4 = 4(1) + b

and resolve for b

4 = 4 + b so b = 0

then our final linear equation will be

y = 4x + 0 = 4x

In conclusion, the equation of the graph is

y = 4x