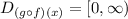The given functions are

To find the first composition, we have to replace the x-variable of f(x) with the function g(x).
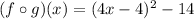
Then, use the notable product to simpligy.
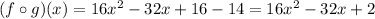
So, the first composition is
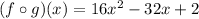
The domain of g(x) is all real numbers because it's a polynomial function. Also, the range of g(x) is all real numbers, which means the domain of the first composition is all real numbers.
The domain of the first composition is
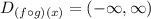
Let's find the second composition and its domain. Repeat the process, substitute the x-variable of g(x) with the function f(x).
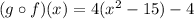
Use the distributive property.
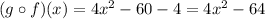
Therefore, the second composition is
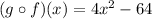
The domain of f(x) is all real numbers but its range is all real numbers greater than or equal to zero. This means the domain of the second composition can take just positive numbers including zero because that's the range of f(x).
Therefore, the domain of the second composition is