Answer
Step-by-step explanation
The area of the hexagon is given as
![\text{Area of the hexagon = }\frac{3\sqrt[]{3}}{2}a^2](https://img.qammunity.org/2023/formulas/mathematics/college/nmtmqq4elap4l4tv77yem4qdqj7bpoamaq.png)
where
a = side of the hexagon, which is the radius of the circle in the image.
Area of the hexagon = 40.8 square inches
![\begin{gathered} \text{Area of the hexagon = }\frac{3\sqrt[]{3}}{2}a^2 \\ 40.8=\frac{3\sqrt[]{3}}{2}a^2 \\ a^2=\frac{2*40.8}{3\sqrt[]{3}} \\ a^2=15.704 \\ \text{Take the square root of both sides} \\ a=3.96\text{ inches} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/chsxyrhuq8vo4a522ui6u94thgxbss44xo.png)
Since the pink area is attached to the hexagon, we can easily calculate its area by noting that it is a sector of a circle with angle of one interior side of the hexagon subtended at the center of the circle.
One interior angle of a haxagon = 120°
Area of a sector is given as
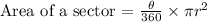
where
θ = Angle subtended by the sector at the center of the circle = 120°
π = pi = 3.14
r = radius of the circle = length of a side of the hexagon = 3.96 inches
![undefined]()