We are given the following expression:
![\frac{\sqrt[4]{y^3}}{\sqrt[5]{y^3}}](https://img.qammunity.org/2023/formulas/mathematics/college/47kcgr39xicjvgnb0elzs94bckjxupp7ac.png)
To convert to rational exponents we will use the following relationship:
![\sqrt[y]{a^x}=a^{(x)/(y)}](https://img.qammunity.org/2023/formulas/mathematics/college/yp2xole0rzgqysvndgfyyixweqc8fgrlcm.png)
Applying the relationship we get;
![\frac{\sqrt[4]{y^3}}{\sqrt[5]{y^3}}=\frac{y^{(3)/(4)}}{y^{(3)/(5)}}](https://img.qammunity.org/2023/formulas/mathematics/college/1xixuh8rosmry8bja7grmu78qfb8aedfeu.png)
Now, we will use the following property of exponents on the denominator:
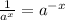
Therefore, we can bring the denominator up by inverting the sign of the exponents, like this:
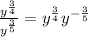
Now, we use the following property of exponents:
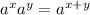
Applying the property we get:
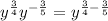
Adding the exponents we get:
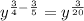
Since we can't simplify any further this is the final answer.