The vertical height (x) represents the point where the slant height (ladder) rest against the wall of the house to the ground level.
The triangle above is a right-angled triangle, we use the pythagorean theorem.
Formula for the Pythagorean theorem is,
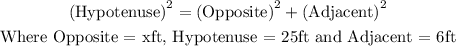
Substituting the variables into the formula above,
![\begin{gathered} 25^2=x^2+6^2 \\ 625=x^2+36 \\ \text{Collect like terms} \\ x^2=625-36 \\ x^2=589 \\ \sqrt[]{x^2}=\sqrt[]{589} \\ x=24.2693ft\approx24.3ft\text{ (one decimal place)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2zx9t9ru6ta9m025yk2hg1907uoxsfxbta.png)
Hence, the ladder is 24.3ft off the ground against the vertical wall.
B is the answer.